How Do You Know if a Residual Plot Is Good
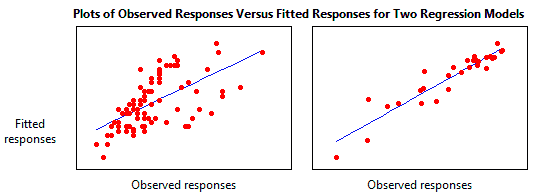
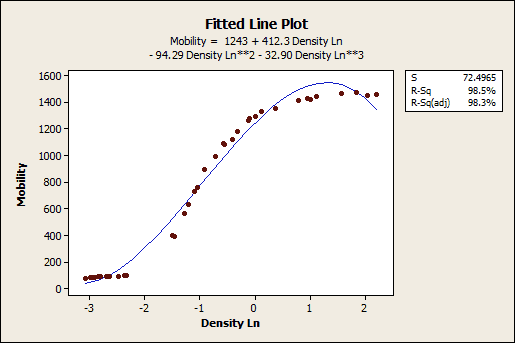
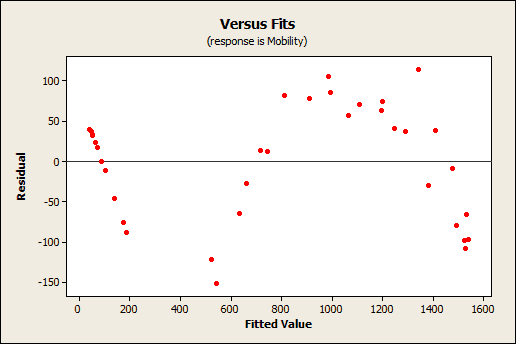
Subsequently you take fit a linear model using regression analysis, ANOVA, or blueprint of experiments (DOE), you need to determine how well the model fits the data. To assistance you out, Minitab statistical software presents a diversity of goodness-of-fit statistics. In this post, nosotros'll explore the R-squared (Rii ) statistic, some of its limitations, and uncover some surprises along the way. For instance, low R-squared values are not always bad and high R-squared values are not always good! Linear regression calculates an equation that minimizes the distance between the fitted line and all of the data points. Technically, ordinary least squares (OLS) regression minimizes the sum of the squared residuals. In general, a model fits the data well if the differences between the observed values and the model's predicted values are small and unbiased. Before you look at the statistical measures for goodness-of-fit, y'all should check the residuum plots. Balance plots can reveal unwanted residual patterns that indicate biased results more effectively than numbers. When your residual plots pass muster, y'all tin can trust your numerical results and check the goodness-of-fit statistics. R-squared is a statistical measure of how close the information are to the fitted regression line. Information technology is also known as the coefficient of determination, or the coefficient of multiple determination for multiple regression. The definition of R-squared is fairly straight-forward; information technology is the percent of the response variable variation that is explained by a linear model. Or: R-squared = Explained variation / Full variation R-squared is always between 0 and 100%: In general, the higher the R-squared, the better the model fits your information. Yet, there are important conditions for this guideline that I'll talk almost both in this post and my next mail service. Plotting fitted values past observed values graphically illustrates dissimilar R-squared values for regression models. The regression model on the left accounts for 38.0% of the variance while the one on the right accounts for 87.4%. The more variance that is accounted for past the regression model the closer the data points will fall to the fitted regression line. Theoretically, if a model could explain 100% of the variance, the fitted values would e'er equal the observed values and, therefore, all the data points would fall on the fitted regression line. R-squaredcannot determine whether the coefficient estimates and predictions are biased, which is why you must assess the residual plots. R-squared does not indicate whether a regression model is adequate. You can have a depression R-squared value for a skillful model, or a high R-squared value for a model that does not fit the data! The R-squared in your output is a biased estimate of the population R-squared. No! In that location are two major reasons why information technology can be just fine to have low R-squared values. In some fields, it is entirely expected that your R-squared values volition be low. For case, any field that attempts to predict human behavior, such as psychology, typically has R-squared values lower than 50%. Humans are only harder to predict than, say, concrete processes. Furthermore, if your R-squared value is low but you accept statistically significant predictors, you lot tin withal draw important conclusions nearly how changes in the predictor values are associated with changes in the response value. Regardless of the R-squared, the pregnant coefficients still represent the mean change in the response for one unit of change in the predictor while holding other predictors in the model abiding. Obviously, this type of data tin exist extremely valuable. See a graphical analogy of why a low R-squared doesn't affect the interpretation of significant variables. A low R-squared is most problematic when you lot want to produce predictions that are reasonably precise (accept a minor enough prediction interval). How loftier should the R-squared be for prediction? Well, that depends on your requirements for the width of a prediction interval and how much variability is present in your data. While a high R-squared is required for precise predictions, it'southward not sufficient by itself, as we shall see. No! A high R-squared does non necessarily indicate that the model has a adept fit. That might be a surprise, but wait at the fitted line plot and residual plot below. The fitted line plot displays the human relationship between semiconductor electron mobility and the natural log of the density for real experimental information. The fitted line plot shows that these data follow a nice tight function and the R-squared is 98.5%, which sounds great. Nonetheless, look closer to see how the regression line systematically over and under-predicts the data (bias) at different points forth the bend. You tin can likewise run into patterns in the Residuals versus Fits plot, rather than the randomness that you desire to come across. This indicates a bad fit, and serves as a reminder as to why y'all should e'er check the residual plots. This instance comes from my post about choosing between linear and nonlinear regression. In this example, the respond is to employ nonlinear regression considering linear models are unable to fit the specific curve that these data follow. Nevertheless, like biases can occur when your linear model is missing of import predictors, polynomial terms, and interaction terms. Statisticians call this specification bias, and it is caused past an underspecified model. For this type of bias, you tin can fix the residuals by calculation the proper terms to the model. For more data almost how a high R-squared is not always good a thing, read my mail service Five Reasons Why Your R-squared Can Be As well High. R-squared is a handy, seemingly intuitive measure of how well your linear model fits a gear up of observations. Withal, every bit nosotros saw, R-squared doesn't tell us the entire story. You should evaluate R-squared values in conjunction with residual plots, other model statistics, and discipline cognition in order to round out the picture show (pardon the pun). While R-squared provides an estimate of the force of the human relationship betwixt your model and the response variable, it does not provide a formal hypothesis test for this relationship. The F-test of overall significance determines whether this human relationship is statistically significant. In my next blog, nosotros'll continue with the theme that R-squared by itself is incomplete and await at 2 other types of R-squared: adjusted R-squared and predicted R-squared. These two measures overcome specific issues in club to provide additional information by which you can evaluate your regression model's explanatory ability. For more about R-squared, acquire the answer to this eternal question: How high should R-squared be? If you're learning about regression, read my regression tutorial! What Is Goodness-of-Fit for a Linear Model?
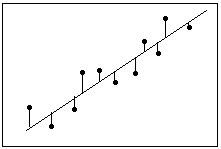Definition: Balance = Observed value - Fitted value What Is R-squared?
Graphical Representation of R-squared
Fundamental Limitations of R-squared
Are Low R-squared Values Inherently Bad?
Are High R-squared Values Inherently Good?
Closing Thoughts on R-squared
Source: https://blog.minitab.com/en/adventures-in-statistics-2/regression-analysis-how-do-i-interpret-r-squared-and-assess-the-goodness-of-fit
0 Response to "How Do You Know if a Residual Plot Is Good"
Post a Comment